Tabel Sin Cos Tan Dalam Perhitungan Ukuran Rumus & Relasi

Hallo guys website rumussoal.com kali ini akan membahas artikel materi tentang tabel sin cos tan sebagai rumus dan relasi dengan perhitungan secara detail beserta ukuran, dan contoh soal agar mudah di pahami dan di mengerti.

Tabel sin cos tan – merupakan rangkaian mengenai tabel yang isinya tentang nilai dari trigonometri yang dapat berfungsi untuk membantu menghitung nilai-nilai yang terdapat pada sudut bangun.

Untuk mengetahui secara detail mengenai dari pengertian serta rumus yang terdapat pada kalimat tersebut maka simaklah mengenai ulasannya di bawah ini …?

Contents hide

1. Sin Cos Tan Adalah

2. Pengertian Sin Cos Tan

3. Rumus Trigonometri

4. Tabel Sin Cos Tan

4.1. Tabel Kuadrat 1 dari 0º Hingga 90º

4.2. Tabel Kuadrat 2 Dari 90º Hingga 180º

4.3. Tabel Kuadrat 3 Dari 180º Hingga 270º

4.4. Tabel Kuadrat 4 Dari 270º Hingga 360º

5. Tabel Bentuk Lingkaran

6. Langkah Cepat Untuk Menghafal Tabel Trigonometri

7. Tabel Trigonometri Untuk Semua Sudut

Sin Cos Tan Adalah

Sin cos tan adalah salah satu fungsi dari trigonometri itu sendiri, sehingga dapat di pastikan bahwa trigonometri sangat terkait dengan Sin cos tan.

Fungsi trigonometri sebagai sin cos dan tan sangat membantu anda ketika menghitung posisi berdasarkan perhitungan trigonometri dasar.

Oleh karena itu, sangat baik bagi siswa dan siswa setingkat SMA untuk memahami dan mengetahui lebih banyak tentang sin cos tan.

karena sin cos tan terkadang keluar dalam Ujian Nasional (UN) di tingkat SMA.

Dengan tabel trigonometri ini, sangat membantu untuk memproses nilai trigonometri dari sudut pandang.

Nilai trigonometri yang dipublikasikan adalah sinus, kosinus, dan garis singgung juga biasa disebut sebagai singkatan sin cos tan.

Baca Juga : Soal Online Matematika Kelas 9

Pengertian Sin Cos Tan

Sebelum Anda melihat tabel nilai-nilai trigonometri cos sin tan, Anda harus terlebih dahulu menjelaskan pengertian atau istilah-istilah sin cos tan dan trigonometri

Sin (sinus) adalah panjang segitiga yang membentuk bagian depan dengan sudut miring y / z.
Cos (cosinus) adalah panjang segitiga antara sisi dan sisi miring x / z.
Tan (tangen) adalah segitiga dengan sisi di depan dan di samping segitiga, y / x.
Trigonometri adalah cabang matematika yang membahas hubungan antara panjang dan sudut dalam segitiga

Agar dapat lebih jelas mengenai pengertian di atas coba kamu perhatikan gambar yang terdapat di bawah ini

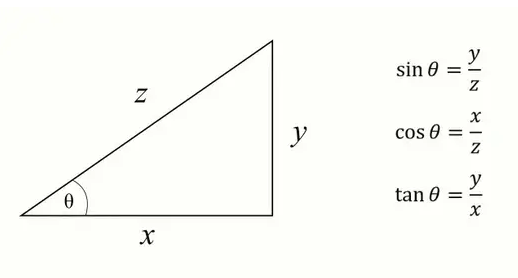
Kesimpulannya : Trgonometri mengenai sin cos tan yang terdapat di atas hanya dapat untuk segitiga yang memiliki sudut 90 derajat atau segitiga siku-siku.

Baca Juga : Soal Online Matematika Kelas 10

Rumus Trigonometri

Trigonometri sendiri memiliki sifat yang unik seperti yang terdapat pada sifat anomali air, namu jika sifat ini di kelompokan dapat di bagi menjadi tiga rumus yaitu:

Kebalikan

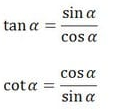
Phytagoras

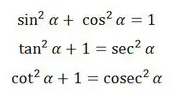
Perbandingan

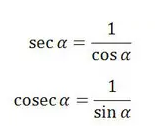
Tabel Sin Cos Tan

Untuk mempermuda kamu dalam menjawab pertanyaan yang berhubungan dengan rumus mengenai trigonometri maka kami akan membuat tabel mengenai sin cos tan.

Dengan sudut satu lingkaran penuh atau biasa di sebut dengan sudut 360 derajat sudut trigometri sendiri terbagi menjadi empat kuadrat.

Tabel Kuadrat 1 dari 0º Hingga 90º

	0º	30º	45º	60º	90º
Sin	0	½	½√2	½√3	1
Cos	1	½√3	½√2	½	0
Tan	0	½√3	1	√3	∞

Tabel Kuadrat 2 Dari 90º Hingga 180º

	90º	120º	135º	150º	180º
Sin	1	½√3	½√2	½	0
Cos	0	–½	–½√2	-½√3	-1
Tan	∞	-√3	-1	-½√3	0

Tabel Kuadrat 3 Dari 180º Hingga 270º

	180º	210º	225º	240º	270º
Sin	0	-½	-½√2	-½√3	–1
Cos	-1	-½√3	-½√2	-½	0
Tan	0	1/3√3	1	√3	∞

Tabel Kuadrat 4 Dari 270º Hingga 360º

	270º	300º	315º	330º	360º
Sin	–1	-½√3	-½√2	-½	0
Cos	0	½	½√2	½√3	1
Tan	∞	-√3	-1	-1/3√3	0

Itulah bentuk dari pada tabel sin cos tan di dalam pelajaran matematika bagi pelajar SMA sederajat.

Yang mungkin dapat berguna dan bermanfaat untuk kalian semua ituk menambah pengetahuan di bidang pelajaran matematika.

Baca Juga : Soal Online Matematika Kelas 7

Tabel Bentuk Lingkaran

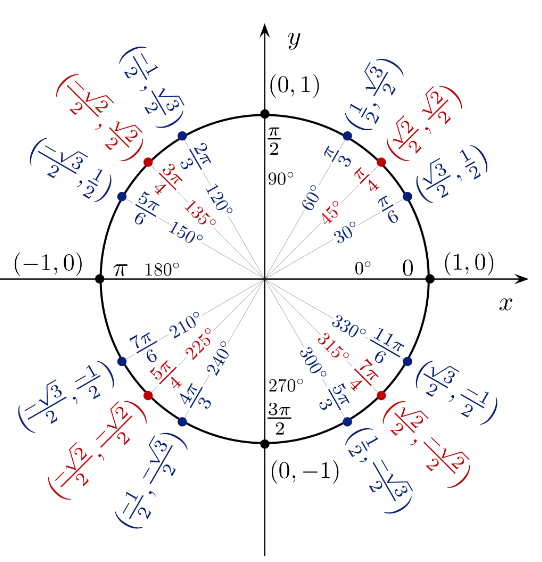
Jika kamu terlalu panjang untuk mengingat tabel sin cos tan yang terdapat di atas dan terasa sulit untuk memahami tentang konsep dari sudut istimewah.

Maka kamu dapat menggunakan tabel trigonometri yang berbentuk lingkaran untuk melihat nilai yang terdapat pada sin cos tan pada sudut 360º

Langkah Cepat Untuk Menghafal Tabel Trigonometri

Selain metode yang disebutkan di atas, ada metode lain yang dapat Anda gunakan untuk dengan mudah mengingat tabel rumus trigonometri.

Anda harus melakukan hal berikut:

Langkah 1 Buat tabel dengan sudut dan kolom dari 0 hingga 90 derajat dengan deskripsi sin cos tan
Langkah 2 Ingat bahwa diagram umum untuk dosa berada pada sudut 0 – 90 derajat √x / 2.
Langkah 3 Ubah nilai x pada √x / 2 di kolom pertama menjadi 0. Pojok kiri atas.
Langkah 4 Isi kolom dengan mengatur x ke 0, 1, 2, 3, 4 di kolom dosa. Jadi, Anda memiliki nilai penuh trigonometri sinus
Langkah 5 Untuk menentukan nilai cos, Anda harus mengubah urutan di kolom dosa.
Langkah 6 Untuk menentukan nilai kecoklatan, Anda harus membuat nilai sinus dengan cos.

Baca Juga : Soal Online Matematika Kelas 7

Tabel Trigonometri Untuk Semua Sudut

Jika tabel di atas menjelaskan bagaimana sin cos tan dihitung menggunakan tabel trigonometri dengan sudut khusus, yaitu dengan sudut khusus seperti 0 °, 30 °, 45 °, 60 ° dan 90 °.

Anda bisa mendapatkan nilai sin cos tan trigonometri dengan cepat karena itu nilai sin cos tan untuk sudut pandang dari 0 ° hingga 360 ° dibahas secara rinci dan terperinci.

sehingga Anda dapat dengan cepat dan efisien menentukan nilai sin cos tan dengan nilai berikut

Sudut	Radian	Sin	Cos	Tan
0°	0	0	1	0
1°	0.01746	0.01746	0.99985	0.01746
2°	0.03492	0.03491	0.99939	0.03494
3°	0.05238	0.05236	0.99863	0.05243
4°	0.06984	0.06979	0.99756	0.06996
5°	0.0873	0.08719	0.99619	0.08752
6°	0.10476	0.10457	0.99452	0.10515
7°	0.12222	0.12192	0.99254	0.12283
8°	0.13968	0.13923	0.99026	0.1406
9°	0.15714	0.1565	0.98768	0.15845
10°	0.1746	0.17372	0.9848	0.1764
11°	0.19206	0.19089	0.98161	0.19446
12°	0.20952	0.20799	0.97813	0.21265
13°	0.22698	0.22504	0.97435	0.23096
14°	0.24444	0.24202	0.97027	0.24943
15°	0.26191	0.25892	0.9659	0.26806
16°	0.27937	0.27575	0.96123	0.28687
17°	0.29683	0.29249	0.95627	0.30586
18°	0.31429	0.30914	0.95102	0.32506
19°	0.33175	0.32569	0.94548	0.34448
20°	0.34921	0.34215	0.93965	0.36413
21°	0.36667	0.35851	0.93353	0.38403
22°	0.38413	0.37475	0.92713	0.40421
23°	0.40159	0.39088	0.92044	0.42467
24°	0.41905	0.40689	0.91348	0.44543
25°	0.43651	0.42278	0.90623	0.46652
26°	0.45397	0.43854	0.89871	0.48796
27°	0.47143	0.45416	0.89092	0.50976
28°	0.48889	0.46965	0.88286	0.53196
29°	0.50635	0.48499	0.87452	0.55458
30°	0.52381	0.50018	0.86592	0.57763
31°	0.54127	0.51523	0.85706	0.60116
32°	0.55873	0.53011	0.84793	0.62518
33°	0.57619	0.54483	0.83854	0.64974
34°	0.59365	0.55939	0.8289	0.67486
35°	0.61111	0.57378	0.81901	0.70057
36°	0.62857	0.58799	0.80887	0.72693
37°	0.64603	0.60202	0.79848	0.75396
38°	0.66349	0.61587	0.78785	0.78172
39°	0.68095	0.62953	0.77697	0.81024
40°	0.69841	0.643	0.76586	0.83958
41°	0.71587	0.65628	0.75452	0.86979
42°	0.73333	0.66935	0.74295	0.90094
43°	0.75079	0.68222	0.73115	0.93308
44°	0.76825	0.69488	0.71913	0.96629
45°	0.78571	0.70733	0.70688	1.00063
46°	0.80318	0.71956	0.69443	1.0362
47°	0.82064	0.73158	0.68176	1.07308
48°	0.8381	0.74337	0.66888	1.11137
49°	0.85556	0.75494	0.6558	1.15117
50°	0.87302	0.76627	0.64252	1.1926
51°	0.89048	0.77737	0.62904	1.2358
52°	0.90794	0.78824	0.61537	1.28091
53°	0.9254	0.79886	0.60152	1.32807
54°	0.94286	0.80924	0.58748	1.37748
55°	0.96032	0.81937	0.57326	1.42932
56°	0.97778	0.82926	0.55887	1.48382
57°	0.99524	0.83889	0.5443	1.54122
58°	1.0127	0.84826	0.52957	1.60179
59°	1.03016	0.85738	0.51468	1.66584
60°	1.04762	0.86624	0.49964	1.73374
61°	1.06508	0.87483	0.48444	1.80587
62°	1.08254	0.88315	0.46909	1.8827
63°	1.1	0.89121	0.4536	1.96476
64°	1.11746	0.89899	0.43797	2.05265
65°	1.13492	0.9065	0.4222	2.14707
66°	1.15238	0.91373	0.40631	2.24884
67°	1.16984	0.92069	0.3903	2.35894
68°	1.1873	0.92736	0.37416	2.4785
69°	1.20476	0.93375	0.35792	2.60887
70°	1.22222	0.93986	0.34156	2.75169
71°	1.23968	0.94568	0.3251	2.90892
72°	1.25714	0.95121	0.30854	3.08299
73°	1.2746	0.95646	0.29188	3.27686
74°	1.29206	0.96141	0.27514	3.49427
75°	1.30952	0.96606	0.25831	3.73993
76°	1.32698	0.97043	0.2414	4.01992
77°	1.34444	0.97449	0.22442	4.34219
78°	1.36191	0.97826	0.20738	4.71734
79°	1.37937	0.98173	0.19026	5.15984
80°	1.39683	0.98491	0.1731	5.68998
81°	1.41429	0.98778	0.15587	6.33709
82°	1.43175	0.99035	0.1386	7.14523
83°	1.44921	0.99262	0.12129	8.18379
84°	1.46667	0.99458	0.10394	9.56868
85°	1.48413	0.99625	0.08656	11.5092
86°	1.50159	0.99761	0.06915	14.4259
87°	1.51905	0.99866	0.05173	19.3069
88°	1.53651	0.99941	0.03428	29.153
89°	1.55397	0.99986	0.01683	59.4189
90°	1.57143	1	0	∞

Nah Guya, Sekian yang dapat kami ulas mengenai pembahasan tentang sin cos tan, Dengan adanya pemahaman yang sederhana ini dapat menambah pengetahuan kita semua, sekian dan terima kasih

Baca Artikel Lainnya>>>>>